1. A first order reaction is 75% completed in 100 minutes. What are the rate constant and half life period of the reaction?
t =100 minutes
a = 100
x = 75
(a – x) = (100 – 75) = 25
k = ?
t½ = ?
k = 2.303/t log10 a / (a – x)
k = 2.303 / 100 log10100 / 25
= (2.303 / 100) log104
= 2.303 x 0.6021 / 100
= 1.387 x 10-2
t½ = 0. 693 / k
t½ = 0. 693 / 1.387 x 10-2
= 49.96 minutes
2. Compound A reacts by first order kinetics. At 25°C, the rate constant of the reaction is 0.45 sec-1. What is the half-life period of A at 25°C? What is the time required to have 12.5% unreacted A for first order reaction?
t½ = 0.693 / k
= 0.693 / 0.45
= 1.54 secs
No. of t½ Amount unreacted from 100%
1 50%
2 25%
3 12.5%
Time of three half-life periods = 3 x 1.54
= 4.62 secs
3. Derive rate constant equation for first order reactions.
Consider the reaction
k1
A → Products
Rate of reaction = - d[A] / dt = k1[A]1.0 ... (1)
Where, k1 is the rate constant of the first order reaction.
At the beginning of the reaction, time‘t’ = 0, let the concentration of A be ‘a’ mol.lit–1.
After the reaction has proceeded for some time‘t’, let the concentration of A that has reacted be x mol.lit–1.
The concentration of unreacted A remaining at time‘t’ will be (a – x) mol.lit–1.
The rate of the reaction will be dx / dt. For a first order reaction,
Rate = dx / dt = k1 (a – x) ... (2)
Upon integrating, equation (2) becomes,
∫ dx / (a – x) = k1 ∫ dt
Which is, – ln (a – x) = k1t + C ... (3)
C = integration constant
At time, t = 0, x = 0.
Substituting t and x values in equation (3),
– ln (a – 0) = k1 x 0 + C
Or
C = – ln a.
Substituting C value in equation (3)
– ln (a – x) = k1t – ln a
Rearranging, k1 = 1/t ln a / ( a – x)
Or
k1 = 2.303/t log a / (a – x) . .. (4)
This equation is known as the first order rate constant equation.
4. Discuss the characteristics of a first order reaction.
1. When the concentration of the reactant is increased by ‘n’ times, the rate of reaction is also increased by n times. That is, if the concentration of the reactant is doubled, the rate is doubled.
2. The unit of rate constant of a first order reaction is sec–1 or time–1.

3. The time required to complete a definite fraction of reaction is independent of the initial concentration of the reactant.
If t1/u is the time of one ‘u’ th fraction of reaction to take place then from equation
k1 = 2.303/ t log a / a – x,
Since k1 = rate constant, t1/u is independent of initial concentration ‘a’.
5. Explain the experimental determination of rate constant for the decomposition of hydrogen peroxide in aqueous solutions.
Pt
H2O2 → H2O + ½O2
The decomposition of H2O2 in aqueous medium in the presence of Pt catalyst follows a first order reaction. The progress of the reaction is followed by titrating equal volumes of the reaction mixture at regular time intervals against standard KMnO4 solution.
Since volume of KMnO4 used in the titration is a measure of concentration of undecomposed H2O2, volume of KMnO4 consumed at t = 0 is ‘Vo’ which is proportional to ‘a’, the initial concentration of H2O2.
Vt is the volume of KMnO4 consumed after time‘t’ of the reaction. Vt is proportional to unreacted H2O2 which is similar to (a – x).
Similarly (Vo - Vt) is proportional to ‘x’; the concentration of H2O2 reacted in time interval‘t’. The first order rate constant ‘k1’ of the reaction is,
k1 = 2.303/ t log Vo / Vt sec–1.
6. Explain the experimental determination of rate constant of acid hydrolysis of methyl acetate
The acid catalysed hydrolysis of an ester follows pseudo first order kinetics. The reaction can be represented as:
H+
CH3COOCH3 + H2O ⇌ CH3COOH + CH3OH
The overall rate of the reaction depends on the concentrations of reactants and also on the catalyst concentration.
Rate = k3 [ester] [H2O] [H+]
Procedure
1. Initially to a definite volume of (100 ml) hydrochloric acid (0.5 N), 10 ml of ester is added and the start of the reaction corresponds to time of addition of ester.
2. The rate of the reaction is followed by withdrawing a definite volume of the reaction mixture consisting of the ester and acid at various time intervals and arresting the further progress of reaction by adding ice. The whole cold mixture is titrated with standard NaOH (0.1 N) using phenolphthalein as the indicator.
3. Let the volume of alkali consumed at t = 0 be Vo cc which is equivalent to the amount of hydrochloric acid present in the definite volume of the reaction mixture drawn out at regular intervals of time.
4. If Vt cc is the volume of alkali consumed for the same definite volume of the reaction mixture drawn out after reaction time ‘t’, then (Vt - Vo) cc is equivalent to the acetic acid produced by the hydrolysis of ester in time ‘t’.
5. A final titration is done after about 8 hours or after refluxing the solution for 45 mins to complete the hydrolysis which is V∞ cc. (V∞ – Vo) cc is equivalent to acetic acid produced from complete hydrolysis of ester.
Calculations
The initial concentration of ester = a a (V∞– Vo) cc
Concentration of ester reacted at‘t’ = x a (Vt – Vo) cc
Concentration of ester remaining at time‘t’ = (a – x) a (V∞ – Vt)
a / (a - x) = (V∞ - Vo) / (V∞ - Vt)
The first order rate expression for the hydrolysis of ester can be written as
k = 2.303 / t log10 (V∞ - Vo) / (V∞ - Vt)
By substituting Vt values for various‘t’ values, k is determined. These values are found to be constant indicating k as the rate constant of the reaction.
7. Explain various types of complex reactions and give one example for each. Or Write notes on (i) consecutive reactions, (ii) parallel reactions and (iii) opposing reactions.
(i) Consecutive reactions
The reactions in which the reactant forms an intermediate and the intermediate forms the product in one or many subsequent reactions are called as consecutive or sequential reactions. In such reactions the product is not formed directly from the reactant. Various steps in the consecutive reaction are shown as below:
k1 k2
A → B → C
A = reactant; B = intermediate; C = product.
Initially only the reactant A will be present. As the reaction starts, A produces an intermediate B through k1 rate constant. As and when B is formed, it produces the product C through k2 rate constant. After the completion of reaction only ‘C’ is present and concentrations of A and B will be zero.
Example: Saponification of a diester in presence of an alkali
k1 k2
R'OOC– (CH2)n–COOR → R'OOC–(CH2)n–COOH → HOOC – (CH2)n – COOH
(ii) Parallel reactions
In these group of reactions, one or more reactants react simultaneously in two or more pathways to give two or more products. The parallel reactions are also called as side reactions.
The reactant A reacts to give products B, C, D separately by following three different reaction pathways involving different k1, k2, k3 rate constants respectively. Among the many side reactions, the reaction in which maximum yield of the product obtained is called as the main or major reaction while the other reactions are called as side or parallel reactions.
Examples:
1. Bromination of bromobenzene:
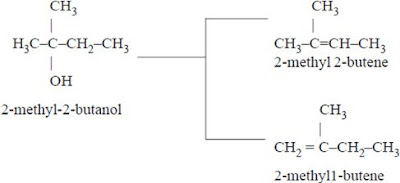
2. Dehydration of 2-methyl-2-butanol
(iii) Opposing reactions
In opposing reactions the products formed react back simultaneously to form the reactants. These reactions are also called as reversible reactions.
kf
A + B ⇌ C + D,
kr
Examples:
1. Reaction between CO and NO2 gases
CO(g) + NO2(g) ⇌ CO2(g) + NO(g)
2. Isomerisation of cyclopropane to propene
3. Dissociation of hydrogen iodide in gas phase
2HI(g) ⇌ H2(g) + I2(g)
8. Give / State / Write the characteristics of order of a reaction.
1. The magnitude of order of a reaction may be zero, or fractional or integral values. For an elementary reaction, its order is never fractional since it is a one step process.
2. Order of a reaction should be determined only by experiments. It cannot be predicted in terms of stoichiometry of reactants and products.
3. Simple reactions possess low values of order like n = 0, 1, 2. Reactions with order greater than or equal to 3.0 are called complex reactions. Higher order reactions are rare.
4. Some reactions show fractional order depending on rate.
5. Higher order reactions may be experimentally converted into simpler order (pseudo) reactions by using excess concentrations of one or more reactants.
9. In the thermal decomposition of N2O at 764°C, the time required to decompose half of the reactant was 263 seconds, when the initial pressure was 290 mm of Hg and 212 seconds at an initial pressure of 360 mm of Hg. What is the order of this reaction?
a1 = 290 mm of Hg
t1 = 263 seconds
a2 = 360 mm of Hg
t2 = 212 seconds
t1/ t2 = ( a2 / a1)n-1
263 / 212 = (360 / 290)n-1
1.24 = (1.24)n–1
n – 1 = 1
n = 1 + 1 = 2
Hence, the reaction is of second order.
10. State the differences between simple and complex reactions.
S.No
|
Simple reactions
|
Complex reactions
|
1
|
Occurs in single step
|
Occurs in multi (or) many steps.
|
2
|
Overall order values are small. Total and pseudo order values lie between 0, 1, 2 and 3.
|
Overall order values are large and greater than 3.0. Sometimes fractional orders such as 1/2, 1/3, 3/2 etc. are seen.
|
3
|
No side reactions
|
Many side reactions are present.
|
4
|
Products are formed directly from the reactants
|
In some complex reactions products are not formed in steps directly involving the reactants.
|
5
|
Experimental rate constant values agree with the calculated values. Theories of reaction rates apply well on simple reactions.
|
Experimental overall rate constant values differ from the calculated values. Theories of reaction rates do not agree well on complex reactions.
|
11. How is the rate constant for the decomposition of Nitrogen pentoxide in CCl4 determined?
ONE MARKS THREE MARKS




No comments:
Post a Comment